Newsletter Volume 10, Issue 3 September 2025

 

Professor, Marine and Civil Engineering Department
Odessa National Maritime University, Odessa, Ukraine

 

Introduction

In many complex engineering projects, there are high soil-retaining structures of essential rigidity. Particularly, it relates to deep-water quay walls designed for huge modern vessels (tankers, container carriers, etc.).

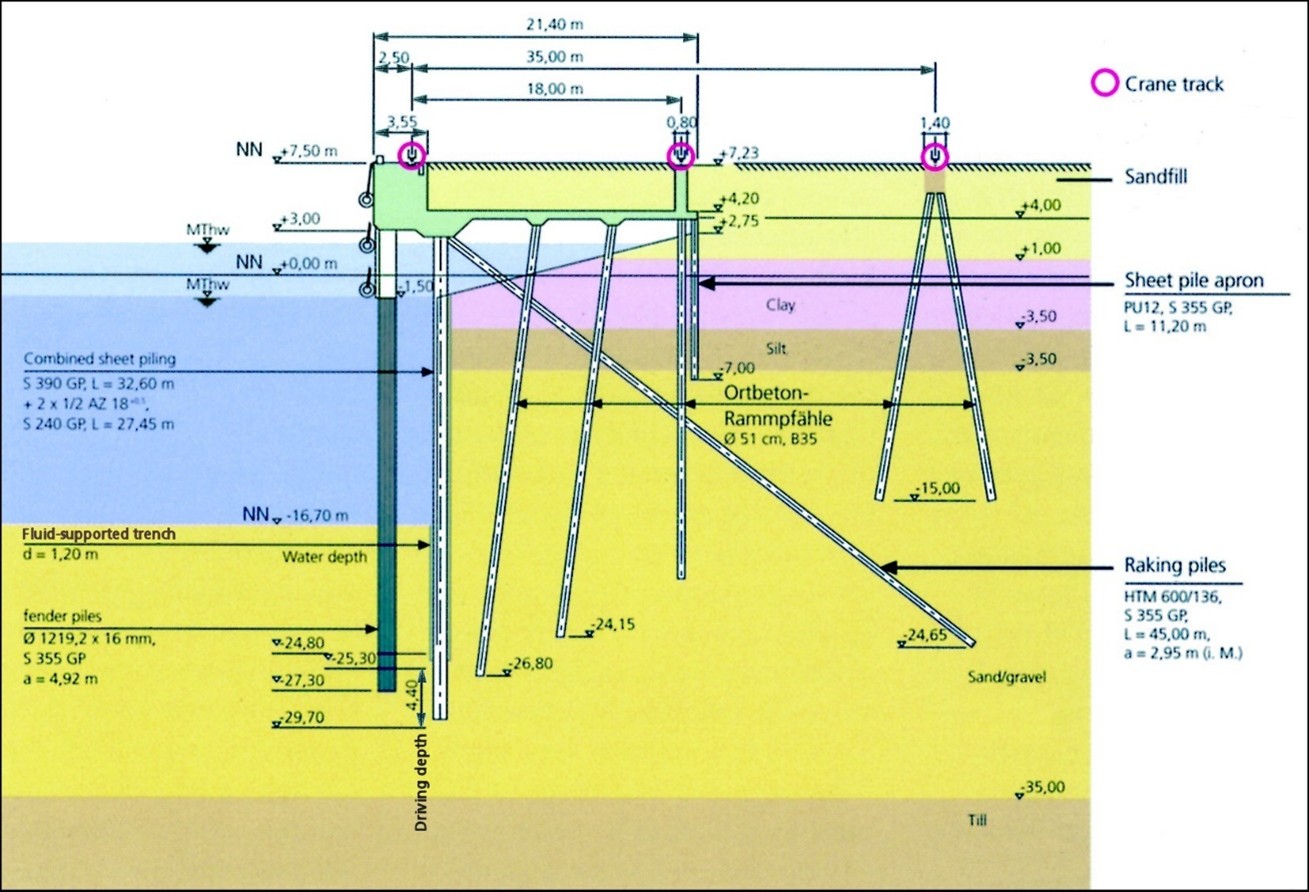
Specific constructions of such quay walls were developed and implemented over the last few decades in some deep-water ports. The required high rigidity of the quay walls was provided using sheet piling sections of very high values of moment of inertia and section modulus.  Among them, we may mention combined sheet pile sections, including king piles of high bearing capacity and ordinary sheet piles, and bearing piles made of universal beams (I section) or pipes. The example of such an approach is presented in Fig. 1.
 

Fig. 1. Container terminal Altenwerder in the Port of Hamburg, Germany

Such structures are filled with various sheet piles and anchor devices. This determines the specificity of their interaction with the soil media, which must be reflected in the design and calculation methods. Some heavy profiles of very high bearing capacity are demonstrated in Fig. 2.

 

GIKEN LTD. has provided effective high quay walls and rigid retaining walls solutions for civil, coastal, and port engineering, i.e.:

• Tubular Pile Wall - heavy sections for high modulus, robust, and versatile foundation solutions (Fig. 3, left)

• Tubular Pile Wall with Interlocks - clutched high modulus tubular pile wall system (Fig. 3, right)

•  King Post Combi-wall - universal beams (I sections) and U sheet pile wall (Fig. 4, left)

• Combi-Gyro Wall - tubular piles and Z or U sheet pile wall (Fig. 4, right)

Fig. 3. Tubular Pile Walls

Fig. 4. King Post Combi-wall (left) and Combi-Gyro Wall (right)

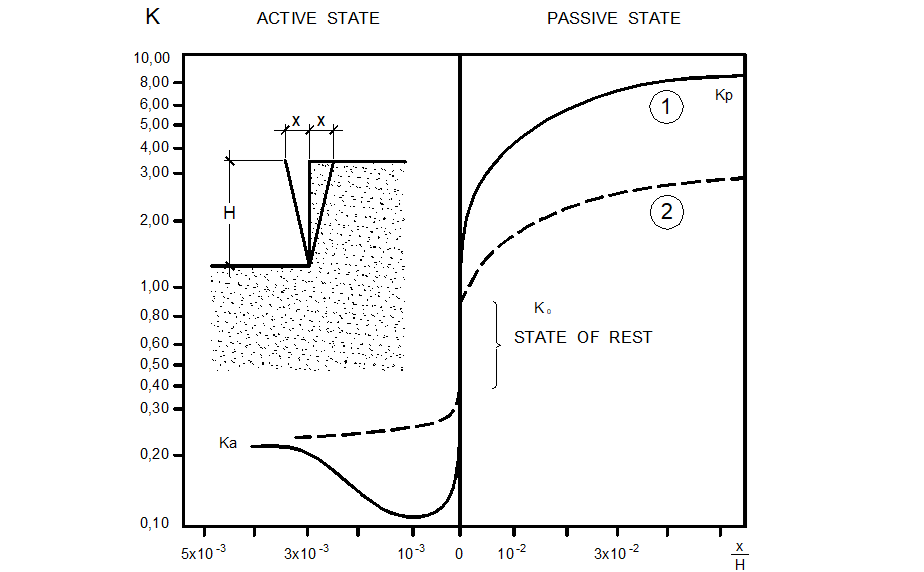
One of the essential peculiarities of the considered system «rigid sheet piling – soil media» is that displacements or deformations are insufficient for the realization of an active and (especially!) passive soil pressure upon the retaining wall. It is known that the stressed state of the soil, even at a motionless wall, can transform starting from the soil pressure at rest and depending on the direction and value of the external loading exerted upon the retaining wall. As an illustration of the mentioned, diagrams from “Maritime works recommendations” [1] (Fig. 5) can serve. Here, the dependencies of the factor of soil lateral pressure on retaining wall deformations (angles of rotation about the bottom end) are reflected. So, soil pressure at rest may be considered as one of the basic characteristics for the analysis of the stressed-deformed state of the system «retaining wall – soil media».
 
From the presentation on Fig. 5 dependencies, it is visible that pressure at rest is defined not by a point on the axis of factors of soil lateral pressure, but a piece on this axis. The curve describing active pressure begins from the bottom border of this piece, and the curve describing reactive soil pressure on a wall starts from its top border. It is necessary to note that the size of this piece is not a constant and depends on the physical characteristics of the soil. For a loose soil, the zone of pressure at rest on an axis of factors of lateral pressure is much more than the zone corresponding to a dense soil.
 
As to Eurocode 7 [2], it supposes the use of certain "intermediate" values of soil lateral pressure when displacements of a retaining wall are insufficient for mobilization of ultimate values. Some European codes recommend calculating soil pressure at rest as active pressure using a conditional angle of internal friction of the soil. It means that above mentioned piece of a zone of rest on an axis of factors of soil lateral pressure on Fig. 5 should be shown as a point conterminous to the bottom end of this piece.

Fig. 5. Dependencies between soil lateral pressure and retaining wall’s deformations

 
Model of interaction retaining wall - soil media
 
Worked-out model is based on the concept of the so-called “threshold of gravitation” [3,4]. It is caused by an inequality of values of soil pressure at rest, corresponding to potential displacement of a retaining wall away from a soil (preliminary stage of active pressure) and towards a soil (preliminary stage of reactive pressure). The physical sense of this parameter may be explained as follows. The soil active wedge is formed almost simultaneously with the beginning of the wall’s displacement because of the action of friction forces that are promoted by the gravity of the soil. At the wall’s displacement towards the soil, its gravity interferes with the displacement. So, only because of overcoming this factor (which is offered to assess numerically by the value of “threshold of gravitation”) action of friction forces in a soil results in the formation of a reactive prism.
 
Based on the known experimental research (for example, [5, 6]), it is possible to assume (similarly to the formation of sliding surfaces corresponding to active or reactive wedges at the wall’s displacement), that some conditional soil wedge corresponds to the soil pressure upon the motionless wall (wedge at rest). As discovered, the sizes of this wedge exceed the dimensions of an active wedge (the last corresponds to the formation of active soil pressure and critical wall’s displacement away from the ground).
 
It is logical to assume that in the case of an opposite direction of construction displacement (towards a soil) dimensions of the wedge at rest will increase, approaching a limit to the sizes of the wedge corresponding to passive pressure. At an initial stage of this process (at the exerting of external loading, but before the beginning of wall displacement towards the soil), there is a rearrangement of the stressed state of the soil interacting with a retaining wall. Thus, the conditional active wedge (stipulated by active soil pressure behind the wall) is transformed to a conditional reactive wedge because an external lateral loading on a wall compensates initial active soil pressure. When external lateral loading on a wall reaches the value capable of causing displacement of a construction towards a soil, the conditional reactive wedge is transformed into a real one. At the moment when reactive pressure reaches the value of passive pressure (at the ultimate state), this reactive wedge can be transferred to the soil bulging wedge. Considered process is characterized not only by an increase in the sizes of the reactive wedge, but also by a change of its geometry because the conditional angle of internal friction (on which geometrical parameters of reactive edge depend) increases (in a limit) up to the value of the angle of internal friction.
 
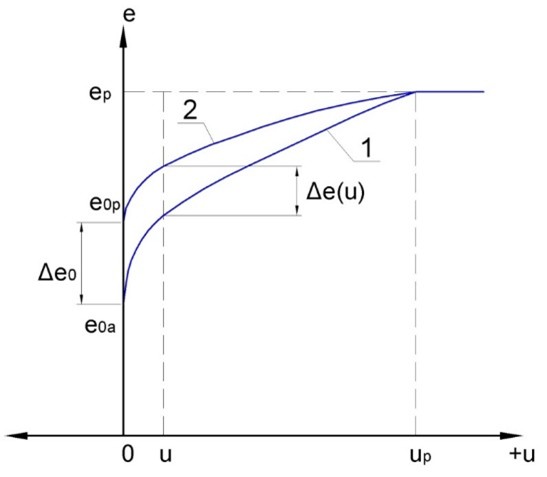
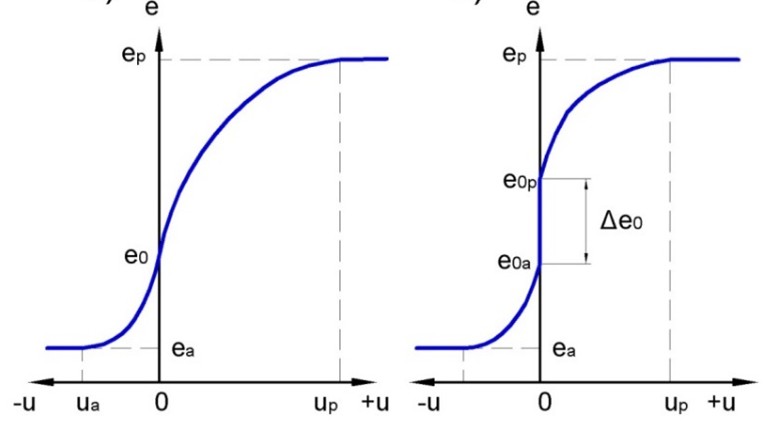
Let’s name the pressure corresponding to the initial stage of formation of soil stressed state regarding potential wall displacement towards the soil (for example, during the initial moment of the exertion on the retaining wall of external lateral loading) as pre-reactive pressure. Similarly, the pressure corresponding to the initial stage of formation of the soil stressed state regarding potential wall displacement away from the soil will be named as pre-active pressure. Hence (regarding above mentioned circumstances), pre-reactive pressure will be more than pre-active one. As pre-reactive pressure (considering its formation and realization) is similar to reactive one (in the ultimate state – to passive pressure), it is expedient to apply formulas related to the calculation of reactive pressure, but using values of the angle of internal friction of the soil, corresponding to its current stressed–deformed state. Thus, the soil stressed state on contact to a motionless retaining wall in researched model is described not by a point e_o on an axis of pressure (as in the traditional approach – Fig. 6a), but by a piece limited from below to value e_oa (the pressure at rest determined on dependences for active pressure), and from above – value e_op (the pressure at rest determined on dependences for reactive pressure) – Fig. 6b.
 

(a)	(b)

  Fig. 6. Dependence of soil lateral pressure on a retaining wall’s displacements

 
Thus, the entered concept of "a threshold of gravitation” can be described by the expression
 

_Δ e_o = e_op - e_oa,

 
where e_op and e_oa  – soil lateral pressure at rest, determined accordingly under formulas for reactive and active pressures.
 
For quantitative assessment of the considered process, the relative parameter can serve (we’ll name it as a factor of the transformation). A factor of the transformation is equal to the ratio of the considered values of soil lateral pressure at rest:
 

K_t = e_op / e_oa.

 
The possible effect of the suggested approach is illustrated by the diagram in Fig. 7, where qualitative dependences «reactive pressure-displacement» for the retaining wall perceiving external loading and moving towards the soil are submitted. Curve 1 corresponds to the pressure at rest, determined under formulas of active pressure, and curve 2 - to the pressure at rest, determined under formulas of reactive pressure.
 
At a motionless wall, the difference between pressure at rest in case of 1 (pressure e_oa) and in case of 2 (pressure e_op) makes «a threshold of gravitation» Δe_o. At formation and increasing of displacements of points on a contact surface of a wall towards a soil the reactive pressure changes in the considered cases according to curve 1 or 2.

Fig. 7. Dependences “reactive pressure–displacements”

 
Thus, the difference Δe (u) of reactive pressure values, corresponding to some moving “u” and caused by various initial soil stressed states (pressure of rest e_oa and e_op) can be rather significant. As calculations show, at a motionless contact surface of a retaining wall, and at values “u” in a vicinity of “zero” displacements, the difference between values of initial pressures e_oa and e_op can reach several hundred percent and essentially influence operating conditions of the whole structure. Accordingly, the value of transformation shows how many times the value of soil lateral pressure at rest increases at the moment just before the beginning of displacement of a retaining wall towards a soil because of the application of external lateral loading to a construction.
 
To calculate values of pressure at rest, it is necessary to use the corresponding values of soil internal friction angle φ_о. In the work of Klein [7], the following dependence was offered:
 

φ_о = arcsin (1-K_o/1+K_o),

 
where K_o is a factor of soil lateral pressure at rest.
 
It would be methodologically correct to link a conditional angle of soil internal friction with its real values. With this purpose Jaki formula can be applied for granulated soils:
 

K_o = 1-sin φ.

 
Given the previous dependence, the formula connecting the conditional and real angles of soil internal friction can be obtained as:
 

φ_о = arcsin [sinφ/(2-sinφ)].

 
Some results of pressure at rest numerical modeling
 

Below some results of the qualitative and quantitative analysis of the data received by numerical modeling of the interaction of elements of the system «a retaining wall - the soil media» are considered. Based on the developed model influence of its base initial data (an angle of internal friction φ and an angle of friction δ of the soil on the contact surface of a wall) on the parameters of soil lateral pressure at rest has been studied.

 
For simplification of the analysis, the retaining wall of gravitational type with a vertical rear contact side and a horizontal unloaded free surface of filling behind of the wall was considered regarding the following intervals of angles φ and δ: φ = 22⁰, 24⁰, 26⁰, 28⁰, 30⁰, 32⁰; δ = 0; 0,25φ; 0,5φ; 0,75φ; φ.
 
The resulting lateral pressure of soil upon a construction can be calculated from a known expression:
 

E= 0,5 γ h² K,

 
where γ – unit weight of a soil; h - height of a vertical contact side of a retaining wall; K - factor of lateral pressure of a soil.
 
It is convenient to present the soil lateral pressure caused by its weight in the dimensionless form:
 

e = E/(0,5 γ h²),

 
where: e - the dimensionless force of lateral pressure of the ground, numerically equal to the factor of corresponding lateral pressure (active, passive, or at rest).
 
The numerical analysis was executed for both flat and curvilinear surfaces of soil sliding. Formulas for calculating soil lateral pressure for the considered wall can be obtained from known, more general dependencies [3, 8, 10].
 
Some results of the numerical analysis of soil lateral pressure at rest on a retaining wall are presented in Table 1. The basic qualitative conclusion from Table 1 is that with the increase of value of φ and δ the value of "a threshold of gravitation» and, accordingly, a factor of transformation, also increases.

 

	flat surfaces of sliding			curvilinear surfaces of sliding
	influence of an angle of internal friction φ (values interval 220-320)
	no contact friction (δ = 0)	full contact friction (δ = φ)	no contact friction (δ = 0)		full contact friction (δ =φ)
Increase of factor of soil lateral pressure	1,10 - 1,61	1,81 - 3,30	1,10 - 1,61		1,71 - 2,91
Increase of factor of transformation	2,80 - 4,36	4,45 - 8,93	2,80 - 4,36		4,10 - 7,66
	influence of an angle of contact friction δ (values interval 0 – φ)
	φ=240- 320			φ=240- 320
Increase of the threshold Δe	1,68 - 2,05			1,59 - 1,81
Increase of the factor of transformation	1,59 – 2,047			1,46 - 1,76

Table 1. Some results of pressure at rest numerical modelling

 
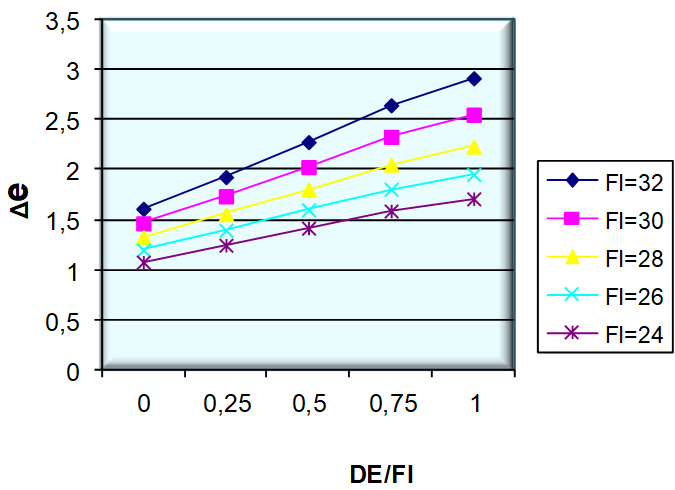
In Fig. 8 and 9 some samples of calculated dependencies are presented for the curvilinear surfaces of sliding.
 

Fig. 8. Dependence between ‘threshold of gravitation’ and angle of soil contact friction

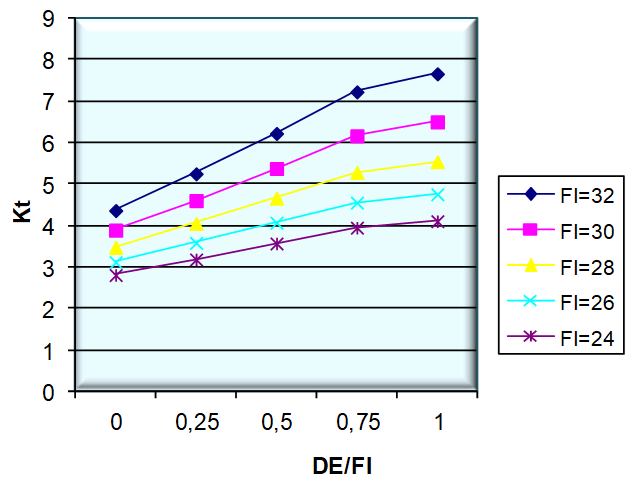
Fig. 9. Dependence between factor of transformation and angle of soil contact friction

 
Соnclusions

Consideration of such concepts as lateral pressure at rest allows taking into account the potential direction of displacement and deformations of a construction.

 

For an estimation of quantitative distinction between "pre-active" and "pre-reactive" soil lateral pressure at rest, such parameters as «a threshold of gravitation» and factor of transformation are proposed and practically implemented in numerical analysis of retaining walls.
 
As "pre-active" soil lateral pressure at rest can exceed "pre-reactive" pressure in times (in an interval from three up to eight times depending on the soil properties), the account of the proposed parameters can increase essentially accuracy of designing and calculating retaining walls and so to affect reliability and technical and economic parameters of constructions.
 
It is determined that an increase of both angles φ and δ is accompanied by an increase in both the «threshold of gravitation» and the factor of transformation.
 
As is known, values of active pressure, calculated both for flat and curvilinear surfaces of sliding, differ insignificantly, but values of reactive (passive) pressure turn out to be more exact (i.e., corresponding to the data of tests) in the case of use of curvilinear surfaces of sliding. In this connection, it may be recommended also to apply the formulas corresponding to curvilinear surfaces of sliding while determining soil pressure at rest and proposed related parameters, i.e.” a threshold of gravitation” and factor of transformation.

 
References

[1] ROM 0.2-90, "Actions in the design of maritime and harbor works," Maritime Works Recommendations, Ministerio de Obras Publicas y transportes, Madrid ,1990.
 
[2] Eurocode 7, Part 1. Geotechnical Design, General Rules. CEN – European Committee for Standardization, 1993.
 
[3] M. Doubrovsky, M. Poizner.  Innovative development of coastal, port and marine engineering: Structures, technologies and design. Lambert Academic Publishing, 2016. 136 p.
 
[4] M. Doubrovsky et al.  Assessment of soil lateral pressure depending on retaining wall displacements. Geotechnology in Harmony with the Global Environment. Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering. Osaka, Japan, 2005. Pp. 889-893.
 
[5] Bugaev V.T., Doubrovsky M.P., Yakovlev P.I., Shtefan A.V. Design of dry docks and their interaction with the soil. Moscow: NEDRA, 2001.
 
[6] P. I. Yakovlev, Stability of Transport Hydraulic Engineering Structures. Transport, Moscow, 1986.
 
[7] Klein G.K. Structural Mechanics of Non-cohesive media. Moscow: STROYIZDAT. 1977.